
Schema acquisition processes comprise an essential source of cognitive demands in learning situations. To shed light on related mechanisms and influencing factors, this study applied a continuous multi-measure approach for cognitive load assessment. In a dual-task setting, a sample of 123 student participants learned visually presented symbol combinations with one of two levels of complexity while memorizing auditorily presented number sequences. Learners’ cognitive load during the learning task was addressed by secondary task performance, prosodic speech parameters (pauses, articulation rate), and physiological markers (heart rate, skin conductance response). While results revealed increasing primary and secondary task performance over the trials, decreases in speech and physiological parameters indicated a reduction in the overall level of cognitive load with task progression. In addition, the robustness of the acquired schemata was confirmed by a transfer task that required participants to apply the obtained symbol combinations. Taken together, the observed pattern of evidence supports the idea of a logarithmically decreasing progression of cognitive load with increasing schema acquisition, and further hints on robust and stable transfer performance, even under enhanced transfer demands. Finally, theoretical and practical consequences consider evidence on desirable difficulties in learning as well as the potential of multimodal cognitive load detection in learning applications.
Interactive learning and training technologies enhance task opportunities in various application domains but may also increase demands on cognitive resources. Arising pitfalls can be avoided by providing systems with knowledge about users’ current mental states, which allows regulating system responses in an adaptive and personalized way. For instance, during learning activities, a system could align features such as the amount and speed of the presented content or the degree of instructional support to increase motivation, encourage sustained performance, and foster system acceptance. Related challenges firstly involve measurement issues, i.e., an accurate user state recognition that requires intelligent algorithms for correctly interpreting patterns contained in the acquired signals. Secondly, the system behavior needs to be continuously adjusted to meet users’ needs in the most sophisticated way possible. The current research provides relevant pre-requisites for both issues by monitoring variations in cognitive demands over the task with a novel combination of sensitive measures related to performance, speech, and physiological reactions. Applying the summarized evidence to real-world applications, dynamic recognition algorithms could be developed for computerized learning devices such as mobile systems that incorporate wearable multimodal sensors.
Looking back in the history of cognitive psychology, there is a long research tradition on cognitive schemata as crucial outcomes of learning processes (Ghosh & Gilboa, 2014). Once knowledge has been acquired successfully, it is represented and organized in small bundles of information that are constructed during learning and applied automatically in later process stages. Research in this field has mainly covered structural aspects (Bartlett, 1932; Rumelhart, 1980) and mechanisms of schema acquisition and adjustment (Piaget, 1952), but less concern was devoted to related demands on learners’ cognitive resources and their changes during the learning process. The current study addresses this research gap by monitoring the interplay of load inducing factors in a controlled learning scenario with a combination of continuous cognitive load measures.
As we consider cognitive resource investment in instructional situations, the Cognitive Load Theory (CLT; Sweller, Van Merriënboer, & Paas, 1998; Sweller, Ayres, & Kalyuga, 2011) becomes an indispensable source of explanation. In brief, the theory resides on three core assumptions: Firstly, based on well-established memory models (Anderson, 1983; Atkinson & Shiffrin, 1971; Baddeley, 1992), it postulates limited working memory resources in terms of duration and capacity of information storage. Secondly, long-term memory resources are assumed to lack such boundaries and hold benefits for elaborated learning processes. Thirdly, mental representation of knowledge should occur via schemata, described as organized knowledge structures with stable patterns of relationships between elements (Kalyuga, 2010). A further characteristic of the theoretical framework is the separation of the overall cognitive load construct into the facets of intrinsic, extraneous, and germane cognitive load (Sweller et al., 1998). Whereas intrinsic cognitive load (ICL) results from the number of interrelated elements of information, determining the complexity of the used learning material relative to learners’ previous knowledge, extraneous cognitive load (ECL) is associated with the surrounding instructional situation, i.e., ways of content presentation or situational constraints. Germane cognitive load (GCL) arises from relevant processes of schema acquisition and automation. Prior research shows that high levels of ECL hamper learning performance, but only if high amounts of ICL are present at the same time (Sweller et al., 1998). Whereas ECL should be minimized and ICL kept at a manageable level, the instructional focus is put on fostering GCL to achieve optimal learning outcomes.
Empirical evidence for the latter approach arises from Wirzberger et al. (2017), who applied a basal learning task that a priori varied the amount of interacting information elements (ICL) and induced interruptions at several points over the task (ECL). Statistical analyses compared linear, quadratic, and logarithmic progression models, and the results suggested a logarithmic progression of schema-related cognitive load (GCL) over time, influenced by structural features. The resulting inversion of the learning curve (Ebbinghaus, 1964) aligns well with established evidence on cognitive skill acquisition (Anderson, 1983; Kraiger, Ford, & Salas, 1993; Shiffrin & Schneider, 1977). It also provides further evidence that building and organizing schematic structures of knowledge in the initial process stages shed higher demands on cognitive resources, whereas automation and tuning procedures in later process stages require smaller resource supplies. Although the approach already yielded promising results, the study raised the need for a more continuous controlled inspection of the determined mechanisms.
Related questions on the durability and robustness of previously established schemata might be addressable by applying acquired knowledge structures on distinct but related problems. Kalyuga (2010) particularly recommends tasks involving grouping or categorizing to create such transfer demands. Evidence on expertise development shows that novice learners require less complex tasks in early training stages to engage in robust and stable schema acquisition (Van Merriënboer, Kester, & Paas, 2006); thus, novice learners dealing with a complex task right from the beginning should perform worse. In addition, extended transfer requirements would overly demand cognitive resources and further decline performance.
Studying the assumed interplay of cognitive load factors requires their valid assessment. Several efforts have been made, relating to performance, psychophysiology, behavior, and self-report (Sweller et al., 2011; Wickens, Hollands, Banbury, & Parasuraman, 2013; Zheng, 2018). From the variety of approaches, a selection will be discussed in the following, which is considered to be relevant for the applied task framework.
Since learners’ performance is explicitly addressed and recorded in learning scenarios, the inspection of performance-related parameters offers valuable insights. Such measures usually operate on observable performance indices in dual-task paradigms that use secondary tasks to induce and/or assess cognitive load (O’Donnell & Eggemeier, 1986). If the secondary task mainly serves to induce cognitive load, primary task performance is observed, whereas the inspection of secondary task performance is applied for purposes of assessing cognitive load (Brünken, Plass, & Leutner, 2004; Brünken, Steinbacher, Plass, & Leutner, 2002; Kraiger et al., 1993; Park & Brünken, 2018). A conjoint observation of both aspects provides a more comprehensive view; thus, often both parameters are inspected complementarily. In terms of task-related stimulus and response modalities, evidence on modality compatibility in dual-task performance shows that for spatial codes a combination of visual input and manual output is superior to auditory input and vocal output, whereas the results are reversed for verbal codes (Hazeltine, Ruthruff, & Remington, 2006). For this reason, when employing dual-task techniques, compatible input and output modalities for both tasks should be used so that resource interference only occurs due to content-related processing demands. Participants’ performance in primary and secondary tasks can further be evaluated in terms of efficiency (Hoffman & Schraw, 2010), with higher levels of efficiency corresponding to high performance and low effort. Efficiency measures usually are calculated from effort indicators like response time, which indicates how cognitively demanding a task was, and performance indicators like correct responses (Sweller et al., 2011).
Bodily functions are often affected involuntarily when people are put under cognitive demands and thus provide reliable online indicators of current levels of cognitive load. Among the variety of psychophysiological techniques, heart rate (HR) and skin conductance response (SCR) have already shown sensitivity to changes in cognitive resource demands in dual-task settings (Mehler, Reimer, & Coughlin, 2012). Both parameters indicate increasing levels of imposed cognitive load by increasing values.
Besides involuntarily occurring bodily responses, participants show voluntarily behavioral reactions as well. The effects of cognitive load on duration-based speech parameters can be classified into the field of prosody, for instance, disfluency, articulation rate, content quality, the number of syllables, and silent pauses as well as filled pauses (Berthold & Jameson, 1999; Müller, Großmann-Hutter, Jameson, Rummer, & Wittig, 2001). Evidence suggests that, with increasing levels of cognitive load, speaking rates (the number of syllables per time) and articulation rates (the number of syllables per time excluding pauses) decrease. More and longer pauses during speech flow, induced by planning processes, also reflect higher levels of cognitive load (Esposito, Stejskal, Smékal, & Bourbakis, 2007; Khawaja, Ruiz, & Chen, 2007, 2008; Müller et al., 2001). So far, the described speech parameters have been applied to determine cognitive load in task settings that demand cognitive resources on a shorter time span, for instance, a reading span task or a Stroop interference task under time pressure (Yap, 2012). A novel perspective arises by applying this approach to capture naturally occurring changes in cognitive resource demands due to schema acquisition processes.
Beneath the introduced objective measures, subjective means of assessment can be applied as well. Self-report rating scales comprise an easily applicable and widely used approach in cognitive load assessment that relies on learners’ ability to provide valid retrospective estimations of the experienced level of cognitive load. A rating scale that addresses the facets of ICL, ECL, and GCL independently was developed by Leppink, Paas, Van der Vleuten, Van Gog, and Van Merriënboer (2013). Higher levels of subjectively experienced cognitive resource demands on each facet are indicated by higher ratings on the related items.
In summary, each measure entails certain strengths and weaknesses (Martin, 2018; Sweller et al., 2011; Wickens et al., 2013). Although performance-related parameters provide a continuous assessment and often emerge directly from the task, secondary tasks potentially interfere with primary tasks and require thoughts regarding the adequate level of complexity as well as the employed stimulus and response modalities. Psychophysiological techniques provide a continuous and reliable assessment, since physiological responses are hardly controllable voluntarily, but these techniques require special equipment, substantial expertise, and effort in application and analysis to avoid and control for artifacts and noise. Behavioral parameters also ensure a continuous and reliable way of assessment but require high expertise and effort as well. While subjective ratings via questionnaires are rather easily applicable, they provide no continuous assessment and rely on participants’ retrospective estimations of prior resource demands. For handling the outlined limitations, a combination of different assessment approaches is therefore regarded as the most promising solution to strengthen the informative value of the emerging results (Chen, Zhou, & Yu, 2018; Korbach, Brünken, & Park, 2018).
To address the outlined research gaps, the current study focused on changes in cognitive load related to the process of schema acquisition, extended by the issue of robustness of the obtained schemata. A basal learning task and a related basal schema application task (Kalyuga, 2010) provided a concise, controllable, and internally valid framework. By combining a set of continuous performance-related, behavioral, and physiological measures, completed by subjective self-reports, the comprehensive capture of underlying cognitive processes was ensured.
Based on the introduced theoretical background, a logarithmically decreasing level of cognitive load with increasing schema acquisition was expected, which should be observable in performance, speech, and physiological parameters (hypothesis 1a). Moreover, an increase in subjectively reported cognitive load with a higher level of task complexity was postulated (hypothesis 1b). Regarding retention and transfer performance, with a higher level of task complexity a decrease in retention performance (hypothesis 2a) and transfer performance (hypothesis 2b) was assumed, as well as a decrease in transfer performance with increasing transfer demands (hypothesis 2c).
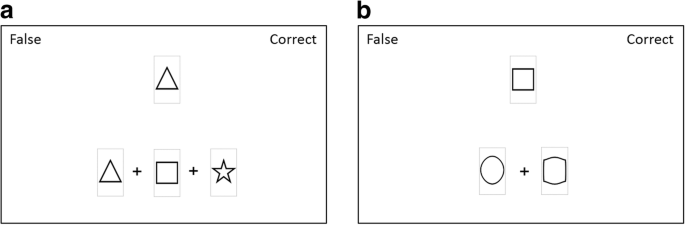
A schema application task was designed to address the robustness of participants’ schema acquisition. It required participants to categorize symbol combinations with reference to a displayed target symbol as either correct or false, according to previously acquired knowledge. Combinations were composed from the four geometrical symbols square, star, triangle, and circle. Some symbol combinations included non-prototypical symbols to determine if the established schemata were stable enough to deal with such kind of transformation. A pre-study should ensure that non-prototypical symbols are still categorized according to their underlying prototype.
Seventy-four participants (Mage = 35.00 years, SDage = 13.09, range 19–64, 63.51% female) completed the test. Of these, 54.05% had already graduated or were currently enrolled as graduate students, 20.27% had completed an apprenticeship, 10.81% were undergraduate students, and the remaining 14.87% reported diverse levels of graduation or did not reveal their educational status.
Non-prototypical symbols were generated with Adobe Photoshop and comprised different severities of either barrel (outward, negative deviation from 0) or pincushion (inward, positive deviation from 0) distortion. As displayed in Fig. 1, the levels of distortion ranged from small (± 30%) to medium (± 60%) to high (± 90%).

Participants filled out an online questionnaire including the prototypical and non-prototypical symbols accompanied with a categorization request. After classifying each symbol as either circle, square, star, or triangle, participants had to rate the level of distortion on a seven-point Likert scale with verbal anchoring at the extreme points to determine the perceived severity of deviation from the underlying prototype. As the prototypes were included in the presented symbol set as well, the scale started from 0 (“not at all”) and reached 6 (“very strong”) to provide participants the opportunity of a valid and reliable rating on a sufficient level of complexity (Lozano, García-Cueto, & Muñiz, 2008).
Descriptive analyses of categorization frequencies and distortion ratings are reported in Table 1. They indicate rather stable and homogeneous classifications of non-prototypical symbols according to their underlying prototype, with at least 94.7% correct categorizations, even on the broader distribution of age and educational backgrounds. Moreover, even on a descriptive level, distortion ratings outline an increasing amount of perceived deviation with increasing severity of distortion.
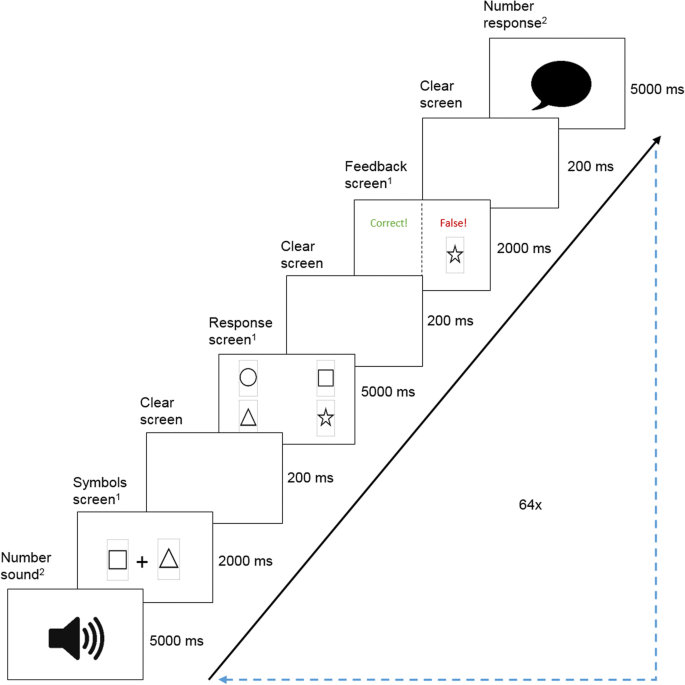
During each of the 60 trials in the schema application task, participants evaluated if the input part of a presented symbol combination matched or mismatched the response part. As depicted in Fig. 3, the response part of the symbol combination was shown in the upper part and the potential input part in the lower part of the screen. Response parts were always represented in prototypical symbols, whereas half of the input parts included distorted symbols from the pre-study. The pool of presented stimuli comprised correctly matched input and target parts, existing input parts with mismatched target parts, and non-existing input parts with mismatched target parts. Within 5 s, participants had to classify the presented combination as false or correct by pressing either the left (false) or right (correct) mouse key. Contrary to the learning task, participants received no further feedback on their response.
For assessing retention performance, participants received a computer-based form with a grid of three (easy condition) or four (difficult condition) empty boxes per combination in four rows. They had to recall the memorized symbol combinations by dragging symbols from an infinite pool for each possible symbol (i.e., circle, square, triangle, or star) via mouse click and dropping them into the existing grid boxes to form combinations. In addition, they could indicate corrections on the provided combinations in a separate comment space below. Participants’ subjectively perceived level of cognitive load was addressed on 11-point Likert scales via the 10-item questionnaire by Leppink et al. (2013) that differs between the three subscales of ICL, ECL, and GCL.
Data were obtained in individual testing sessions of about 60 min in a separate laboratory, equipped with a standard desktop computer for the participant and an experimenter netbook to record the physiological data. At the outset of each testing session, participants were welcomed and signed an informed consent. This form outlined the purpose and procedure of the study and ensured that participants’ treatment aligned with approved ethical standards and that their privacy was respected. Afterward, the OSPAN had to be completed, which usually took about 15 min. Before starting the learning task, the experimenter had to fulfill several preparatory duties, requiring about 5 min. First, the electrodes for the physiological measures were attached to the left hand and a close-talk microphone for the speech recording was placed at the upper part of the participant’s sternum. Following an initial adjustment of the speech recording volume to individual voice characteristics, the learning task was completed within an average duration of 20 min. After the electrodes were removed, participants worked on the questionnaires on retention, cognitive load, and demographics, which were provided online and were completed in about 10 min by most participants. Finally, they completed the schema application task (about 10 min) and were debriefed and approved.
Primary task efficiency was computed, following the likelihood model (Hoffman & Schraw, 2010), as the quotient of correct responses (performance) and reaction times (effort) within each trial. Since reaction times were retrieved in milliseconds, scores were multiplied by 1000 to obtain the proportion of correct responses per second. The resulting values provide a hint on the investment of available mental resources over the task: if learners start to perform faster and less erroneously on the task, they must invest less mental capacity.
For secondary task efficiency, also based on the likelihood model approach (Hoffman & Schraw, 2010), performance was computed by comparing spoken words to correct words from the reference and subtracting the amount of substituted, deleted, and inserted words (Lee, 1988) relative to the total number of words in the reference (word accuracy). The participant’s effort was reflected in the time starting from the presentation of the visual stimulus to the end of the last uttered digit (verbal response duration), which covered the entire answer process.
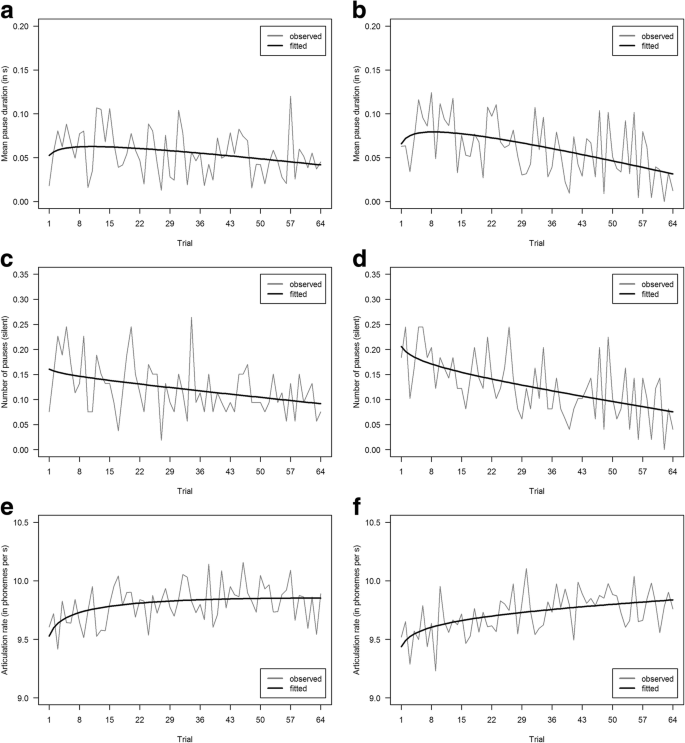
Speech parameters were extracted on the phoneme level using an automatic speech recognition system (Herms, 2016). The resulting transcripts included spoken units and the corresponding time codes in milliseconds and were used to derive the articulation rate, the number, and the mean duration of silent pauses. The articulation rate represented the total number of phonemes divided by the utterance duration excluding the total duration of silent pauses, the number of pauses reflected the total number of silent pauses in an utterance, and the mean pause duration was calculated from the total duration divided by the number of silent pauses.
Physiological data were recorded at a frequency of 128 Hz with a NeXus-10 Mark II from sensors attached to the volar surface of the distal phalanges of the left hand. While the heart rate (HR) signal was obtained at the trigger finger, the skin conductance response (SCR) was recorded at the middle and ring fingers. Data preparation involved the calculation of an individual baseline for each participant from values located in the preparation phase of about 5 min before starting the learning task. Recorded SCR and HR values were normalized to the individual baseline value and aggregated on mean values for events within each trial. Each event represented a subtask within the learning trial and was related to a screen change, i.e., the auditory presentation of a number sequence, the visual presentation of the symbol combination input, the response part of the presented symbol combination, a feedback on the given response, and finally the verbal recall of the memorized number sequence.
For obtaining retention performance, sum scores were calculated for all memorized symbol combinations and all correctly memorized symbol combinations, resulting in values ranging from 0 (neither combination memorized correctly) to 4 (all combinations memorized correctly). Transfer performance was obtained from the schema application task in terms of reaction times on the provided classifications as well as correct responses. The latter were adjusted for inherited errors from the retention task.
Cognitive load scores were derived from sum scores for each cognitive load facet, resulting in a maximum of 30 points for ICL and ECL and a maximum of 40 points for GCL. Subscales achieved satisfying internal consistencies of α = .831 for ICL, α = .708 for ECL, and α = .876 for GCL. In line with Conway et al. (2005), who reported a clear advantage of partial credit scoring procedures over all-or-nothing scoring procedures, the partial load score for the OSPAN was computed by awarding one point for each correctly recalled letter. Across the three test blocks, the task achieved an appropriate internal consistency of Cronbach’s α = .805.
Some datasets had to be excluded from data analysis due to missing values or the failure to meet the 85% accuracy criterion in the OSPAN Footnote 1 task, a lack in language proficiency, or an observable violation of the instruction. Conditional growth curve models were computed to inspect progressions in primary and secondary task efficiency from a temporal perspective. Values for all relevant variables were z-standardized to obtain standardized β coefficients. Models were fit with restricted maximum-likelihood estimation and included time, condition, the OSPAN score, and the interaction between time and condition predictors as fixed effects aligned to the experimental task design. To take into account individual differences between participants in reaction to experimental variations, a time slope as well as subject-specific intercepts were considered as random effects and assumed to be correlated. In addition, time was computed as a logarithmic Footnote 2 variable and included as a fixed effect. For evaluating model fit, the root mean squared error (RMSE) was obtained from a leave-one-out-cross-validation approach, and the conditional pseudo R 2 for generalized linear mixed models was calculated.
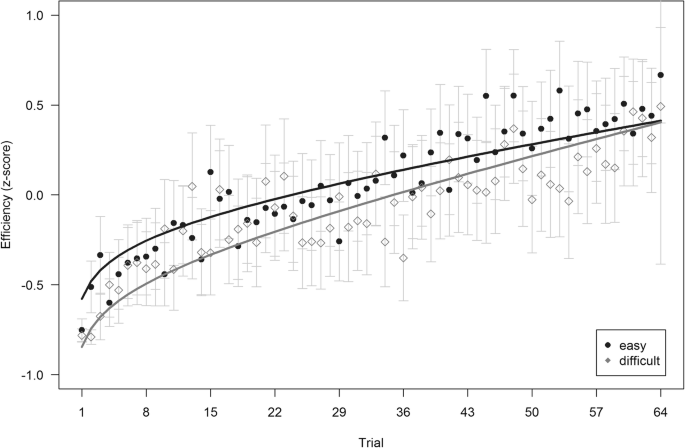
When analyzing secondary task efficiency, one additional dataset had to be excluded from the sample due to high noise in the recorded speech signal, resulting in a subsample of n = 102 participants. Corresponding to the prevention of distraction effects on the primary task from an overly complex secondary task, participants achieved a predominantly high word accuracy (M = 0.95, SD = 0.15). As visually supported by Fig. 5, the results revealed an increasing secondary task performance efficiency over time as well. In more detail, standardized coefficients showed a significant logarithmic time predictor, β = .160, SE = 0.022, t(6323) = 7.392, p < .001, whereas no significance could be obtained for the linear time predictor, β = .029, SE = 0.028, t(361) = 1.022, p = .307, the effect of condition, β = −.044, SE = 0.062, t(99) = − 0.711, p = .479, and the interaction between time and condition, β = −.006, SE = 0.021, t(100) = − 0.271, p = .787. The overall model achieved a considerable fit with RMSE = 0.912 and R 2 = .445 and supports hypothesis 1a.
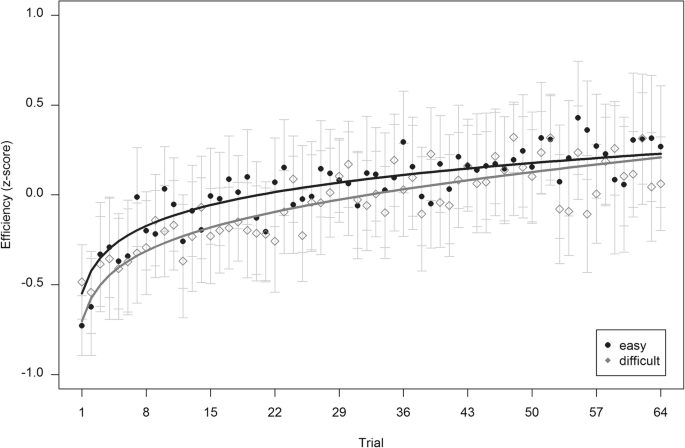
Corresponding to secondary task performance, results are based on n = 102 participants. Time series regressions with linear and logarithmic trend predictors, separated by conditions as depicted in Fig. 6, support decreases in cognitive load over time in terms of mean pause duration, R 2 easy = .063 and R 2 difficult = .216. In terms of number of pauses and articulation rate, the models achieved R 2 easy = .131 and R 2 difficult = .311 for number of pauses and R 2 easy = .165 and R 2 difficult = .268 for articulation rate. Although amounts of explained variance differ between measures and conditions, the overall trend supports hypothesis 1a.
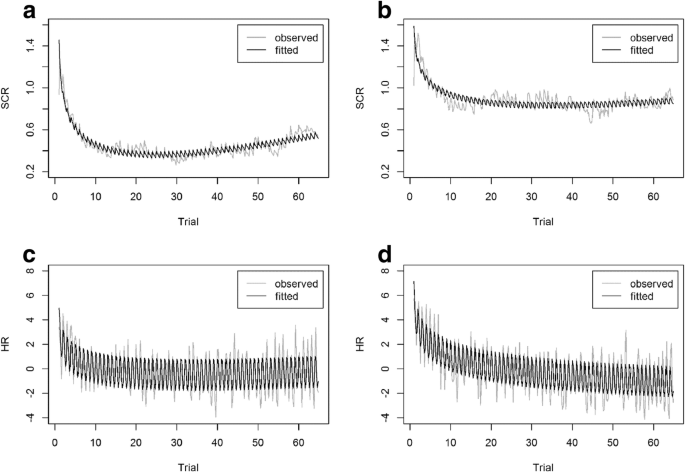
Due to technical errors in the recorded data, two additional datasets had to be excluded from the analysis, resulting in a subsample of n = 101 participants. Assuming additive time series with trend and seasonal components, analyses indicate a decreasing trend of HR and SCR over the task and show a repetitive seasonal pattern across “subtasks” within each trial. Logarithmic time series regression models, including linear and nonlinear trend predictors as well as seasonal predictors, achieved R 2 easy = .847 and R 2 difficult = .672 for SCR, whereas for HR an R 2 easy = .590 and R 2 difficult = .643 could be obtained. Inspecting the seasonal component in more detail, following an initial increase while the sequence of numbers was presented auditorily, a decreasing progression over the symbol presentation, symbol response, and symbol feedback could be observed. However, in the final step of verbally recalling the memorized numbers, physiological response parameters increased again. Fig. 7 displays the respective observed and fitted logarithmic progression curves, which strongly support hypothesis 1a.
Results for both retention and transfer performance are based on n = 103 participants. In terms of retention performance, in line with hypothesis 2a, significantly fewer correctly recalled symbol combinations could be observed in the difficult conditions, t(96.53) = 4.72, p < .001, d = − 0.92. No significant differences between conditions regarding the amount of totally recalled symbol combinations resulted, t(100.99) = − 0.08, p = .937, d = 0.02. A power Footnote 3 level of 1 – β = .71 was achieved for α = .05 and d = 0.5.
As already indicated from the descriptive values in Table 2, results revealed significantly faster responses in the difficult condition, F(1, 101) = 5.59, p = .020, ηp 2 = .05, reversing the pattern postulated in hypothesis 2b. The significant increase in reaction time with increasing distortion, F(3, 303) = 15.13, p < .001, ηp 2 = .13, partially supports hypothesis 2c. A significant interaction between both factors did not result, F(3, 303) = 0.60, p = .614, ηp 2 = .01, 1 – β = 1.0 for α = .05 and f = .25. Post hoc pairwise comparisons using Tukey’s honest significant difference (HSD; Maxwell, 1980) indicate significant differences in reaction time between the prototypical level and all levels of distortion (all p’s < .05) as well as the distortion levels 30 and 90 (p < .001). After correction for inherited errors, no significant differences result in correct responses between conditions, F(1, 101) = 0.99, p = .323, ηp 2 = .01, 1 – β = .941, and levels of distortion, F(3, 303) = 1.42, p = .237, ηp 2 = .01, 1 – β = 1.0. Likewise, no significant interaction between both factors could be detected, F(3, 303) = 0.91, p = .436, ηp 2 = .01, 1 – β = 1.0. All reported power levels relate to α = .05 and f = .25. In general, with around 70% in each level of distortion, a high frequency of correct responses was observable (see Table 2), hinting at a rather stable and robust application of previously acquired schemata.
Table 2 Descriptive values of correct responses and reaction time for levels of distortion in conditions
Contrary to hypothesis 1b, no significant differences between easy and difficult conditions appeared for ICL, t(90.76) = − 1.13, p = .225, d = 0.306, and ECL, t(97.57) = − 1.22, p = .226, d = 0.242, although descriptive values pointed towards lower scores for the easy condition. By contrast, significantly higher ratings in the easy condition resulted for GCL, t(98.77) = 2.87, p = .005, d = − 0.568, which directly reverses the pattern postulated in hypothesis 1b. According to Cohen (1988), the effect amounts to a medium size. Analyses achieved a power of 1 – β = .709 for α = .05 and d = 0.5.
This study provided insight into the progression and interaction of the outlined facets of cognitive load by applying a multi-method approach to cognitive load assessment. In line with the postulated hypothesis, performance, speech, and physiological parameters indicated a logarithmically decreasing level of cognitive load over the task, hinting at increasing progress in schema acquisition. The subjective ratings did not support the initial assumptions, but support arises for the decrease in retention performance with higher levels of task complexity. For transfer performance, the stated hypothesis on increased transfer demands was partly confirmed in terms of reaction times, while evidence indicated a reversed pattern for task complexity in this case.
In addition, physiological measures revealed a repetitive seasonal pattern across the subtask routines for SCR and HR: during the presentation of the auditory stimulus at the outset of each trial, an increase was observable. It was followed by a decrease related to the visual presentation of the symbol combination, the motor response selection, and the visual feedback screen. As soon as the verbal response on the initially presented digit sequence was requested, increasing levels in both physiological measures again resulted. This evidence suggests higher levels of cognitive load imposed by the auditory-verbal compared to the visual-motor stimulus-response combination due to the observable initial and final increase in the emerging signal. Support for this assumption arises from Posner, Nissen, and Klein (1976), who state the dominance and increased familiarity of the visual modality compared to other modalities. Another potential clarification suggests increased perceptual load (Lavie, 2010) in the auditory-verbal secondary task, imposed by the additional visual stimulus from the speaker and speech bubble symbols shown on the screen.
Approaching the obtained pattern in the subjective cognitive load ratings, at least on a descriptive level participants reported lower ICL and ECL. On the one hand, these scores might have lacked statistical significance due to the reported insufficient power level of about 71%. On the other hand, as secondary task requirements did not differ between conditions, the absence of considerable differences in ECL is indeed plausible. Moreover, adding just one symbol to the combination might not have resulted in extensive increases in task complexity, potentially explaining the absence of significant differences in ICL. The reversed pattern for GCL could have originated in the particular formulation of the related questions, which emphasizes the subjective impression of understanding and knowledge acquisition. This might have been higher in the easy condition. The authors (Leppink et al., 2013) also discuss this issue in a more recent publication that applies this questionnaire (Leppink, Paas, Van Gog, Van der Vleuten, & Van Merriënboer, 2014). They attribute the lack of meaningful results for GCL to the substantial redundancy between GCL and ICL and take this as further evidence for the initially outlined re-reduction of the three-factor model. By contrast, a more recently developed cognitive load questionnaire by Klepsch, Schmitz, and Seufert (2017) addresses this issue by including the effort component more explicitly in the GCL facet and advocates the existing three-factor model from an assessment perspective. As the authors claim its applicability for a wider range of learning contexts and domains, using this questionnaire instead would be a valuable extension in future studies.
Regarding the schema application task, faster response times in the difficult condition compared to the easy condition hint at higher investments of mental resources with higher levels of task complexity. This explanation corresponds well with results on contextual interference (de Croock, Van Merriënboer, & Paas, 1998; Van Merriënboer et al., 2006) which report that learners can achieve a more robust and stable transfer performance under conditions that disable fast and easy skill acquisition. Additional support arises from evidence on desirable difficulties in learning situations (Bjork & Bjork, 2011). For instance, when learners must cope with interleaved tasks, they need to maintain sustained engagement of cognitive resources, which fosters performance. The observed increase in response times with increasing distortion may result due to the requirement of additional cognitive operations, as distorted symbols demand the identification of the underlying symbol category before the judgement.
The pattern of evidence supports a temporal extension of the CLT framework and reveals a logarithmically decreasing cognitive load progression with increasing schema acquisition. Moreover, results indicate the benefit of an automatic detection of the current level of cognitive load in speech parameters. This could be of value for realizing adaptive user interfaces in digital learning contexts that bear the ability to adjust task complexity and instructional guidance to learners’ needs and preferences. A particularly promising field of application comprises foreign language learning, where spoken interaction during the learning process constitutes an essential pre-requisite to shape language skills. User-aligned instructional aids within a considered language training program might then entail additional explanations or calming feedback if states of high load are detected by extended pausing or low articulation frequencies.
A potential limitation arises from the differing symbol complexity, since a visually dominating appearance like a star, with salient edges and corners, could foster and speed up schema acquisition and thus benefit symbol recall. More detailed analyses of times spent on drawing different symbols in the retention questionnaire by mouse tracking or gaze pattern analyses might enlighten this issue in future research. With reference to the non-prototypical symbols used for the schema application task, although there was a high level of consensus in the pre-study regarding the correct match to the underlying prototype, subtle differences still could have persisted and influenced the findings in the main task.
The lack of significant differences between conditions in secondary task efficiency could have resulted from task order ambiguities. Although participants were instructed to give equal weight to both tasks, the secondary task occurred first in order and could have been regarded as more easy and familiar. For this reason, participants might have been motivated to prioritize this task instead of the primary task and assign only free resources to the primary task. In consequence, the easy task condition would achieve better results in primary task efficiency, whereas secondary task performance would stay unaffected by task complexity. The choice of keeping this fixed presentation order across all trials and participants is aligned to the original task procedure reported for automated complex span tasks (Redick et al., 2012; Unsworth et al., 2005). Using a counterbalanced presentation order instead could result in more balanced weighting of the priority of both tasks in future studies. A further valuable extension could address the relationship between both tasks more explicitly to obtain insights into participants’ strategies of cognitive resource distribution. The additional use of cognitive models (Anderson, 1983) that compare both task order strategies could support the clarification of distinct effects of task order prioritization.
Prospective research should monitor learners’ focus on presented symbols or alternative learning material by inspecting gaze behavior in combination with pupil dilation, as suggested by Foroughi, Sibley, and Coyne (2017) and Mitra, McNeal, and Bondell (2017). Another promising extension incorporates the transfer of the obtained patterns and mechanisms to more applied task settings in a different task domain like motor learning. In this domain, an additional step could involve the inclusion of a spatial dimension or the use of animated stimuli or motor sequences, and distinct audio-verbal secondary tasks with a different task order are suitable as well. A further interesting extension takes evidence on modality compatibility in dual-task settings (Hazeltine et al., 2006) into account and inspects the use of incompatible content-modality matchings.
The study applied a multi-measure framework of cognitive load assessment to gain further insights into the temporal progression of cognitive load during schema acquisition. Results replicate the logarithmic pattern of change over the task observed in prior research and reveal influences of task complexity and situational constraints. In summary, the promising approach holds value to address existing research gaps in cognitive load research and gain better insights into changing demands from schema acquisition in learning settings.
This exclusion involved seven participants, which corresponds to about 6% of the sample. For comparison, Unsworth et al. (2005) report exclusion rates of 15%.
In line with Wirzberger et al. (2017), alternative linear and quadratic progression models were tested as well, but not reported due to the confirmed advantage of the logarithmic model and the lack of benefit for the focus of this study.
Power analyses refer to theoretically assumed population effect sizes to provide a broader informative value for the reasoning about non-significant results (O'Keefe, 2007).
Analysis of variance
Cognitive load theory
Extraneous cognitive load
Germane cognitive load
Honest significant difference
Intrinsic cognitive load
Operation span task
Root mean squared error
Skin conductance response
Science, Technology, Engineering, and Mathematics
Thanks to Robert Alig and Laura Seelig for their help with data collection and preparation.
The reported research was conducted with funding from the German Research Foundation/DFG grant GRK 1780/1. The publication costs of this article were funded by the German Research Foundation/DFG and TU Chemnitz in the funding program Open Access Publishing.
The materials and the datasets analyzed during the study are available on request.